带有 Python 脚本的 Scientific Linux 7.1 上的矢量代数:第 1 部分
在此页
- 向量代数
- 幅度
- 方向
- 方向
- 向量代数和
- 向量乘以标量
- 单位向量
- 线性组合
- 向量的大小
- 向量的方向
- 向量的方向
- 向量代数和
- 向量乘以标量
- 单位向量
- 线性组合
在本教程中,我们将讨论 Scientific Linux 下的向量代数和相应的计算。出于我们的目的,我选择了 Python 作为编程语言,因为它的简单性和计算能力。默认情况下,任何 Linux 发行版都有一个通过终端窗口调用的 Python 编辑器/编译器。让我们回顾一下向量代数的一些概念。
注意:我们只处理二维或三维的真实空间。
矢量代数
从数学的角度来看,向量空间的元素可以表示为属于该向量空间的多个元素的数组。更具体地说,在数值计算方法中,它可以表示为实数列表,具有三个基本特征:
震级

X、Y 和 Z 是矢量坐标。
方向
向量的方向由准线给出,准线对于坐标系的每个轴具有特定角度,称为导向角。
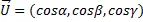
其中 alpha、beta 和 gamma 是矢量指向角,它们的余弦是指向余弦,它们也可以通过将每个矢量坐标除以其大小来计算。
方向
同一方向之间的两个可能方向之一。
向量代数和
要计算向量的代数和,我们必须将两个向量的同源坐标相加,并具有实数代数和的相同性质。如下:
向量乘以标量
给定一个向量和一个标量,标量乘积向量定义为向量每个坐标的标量积:
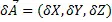
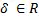
单位向量
标量对 Product 向量的直接应用是单位向量,a字母间距:正常;行高:22.3999996185303px;孤儿:自动;文本对齐:开始;文本缩进:0;文本转换:无;空白:正常;寡妇:1;字间距:0 ;-webkit-text-stroke-width:0;background-color:#fff>unit vector 是长度为 1 的赋范向量。
线性组合
当我们将过去的操作,代数和和乘积向量-标量混合时,我们得到一个线性组合,其中的结果也是属于同一个向量空间的向量,如下:
其中向量 A 是向量 B 和 C 的线性组合。
Scientific Linux 7.1 上的 Python
为了实现矢量代数,我们选择了 Python 作为微积分语言。我们选择的文本编辑器是 gedit,默认情况下随发行版 Scientific Linux 7.1 一起提供。
矢量的大小
让我们使用终端调用 gedit 或只需单击应用程序选项卡上的图标:
V=[2, 2, 1]让我们声明一个变量来存储幅度并给出一个值,我们使用 0。
modV=0现在我们使用类 math 来运算平方根:
import math量级的计算:
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)正如我们所见,我们必须使用子索引来表示我们将要操作的列表中的项目,从0开始。
完整的脚本如下:V=[2, 2, 1]
modV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
print (modV)完成后,我们必须使用扩展名 .py 保存文件并找到文件路径,然后右键单击打开终端窗口,然后“在终端窗口中打开”。在我们必须调用 python 解释器键入之后:
$ python [path]/yourfilename.py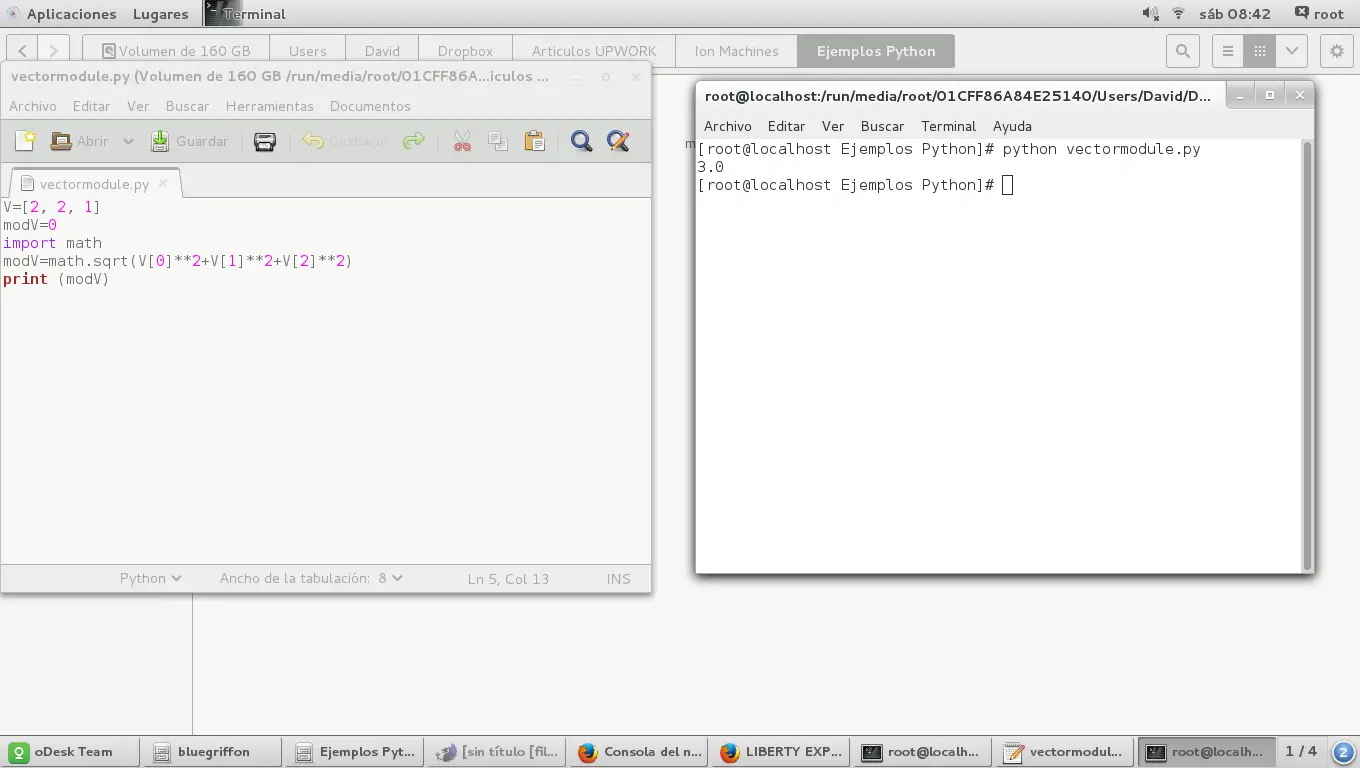
for x in range (0,3):
modV+=V[x]**2
modV=math.sqrt(modV)在这里我们必须使用缩进技术,因为 python 解释器以这种方式工作。
矢量的方向
使用课堂数学
V=[2, 1, 2]
modV=0
import math
for x in range (0,3): #loop for calculating the magnitude
modV+=V[x]**2
modV=math.sqrt(modV)
for y in range (0,3): #loop for calculating the director cosines
V[y]=V[y]/modV
print (V)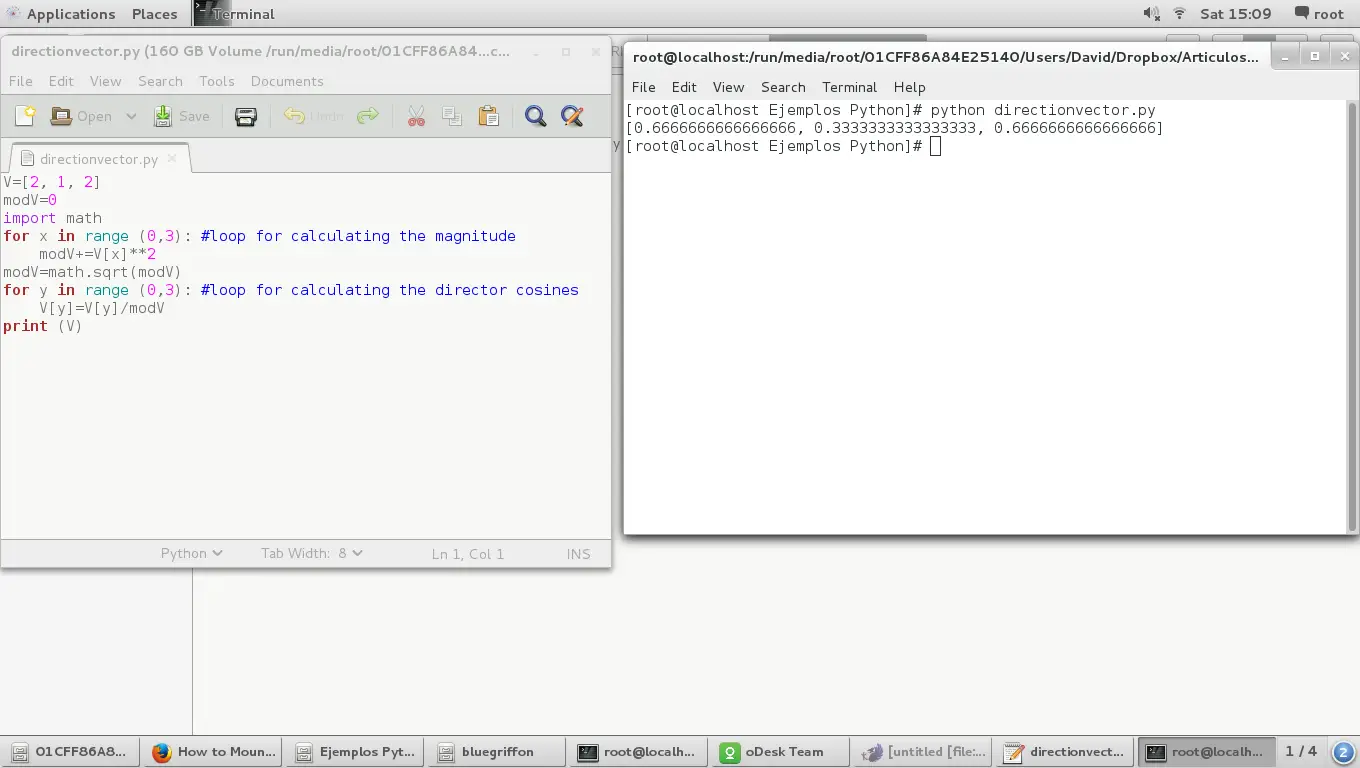
V=[2, 1, 2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))然后让我们计算导演余弦并打印出来
for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)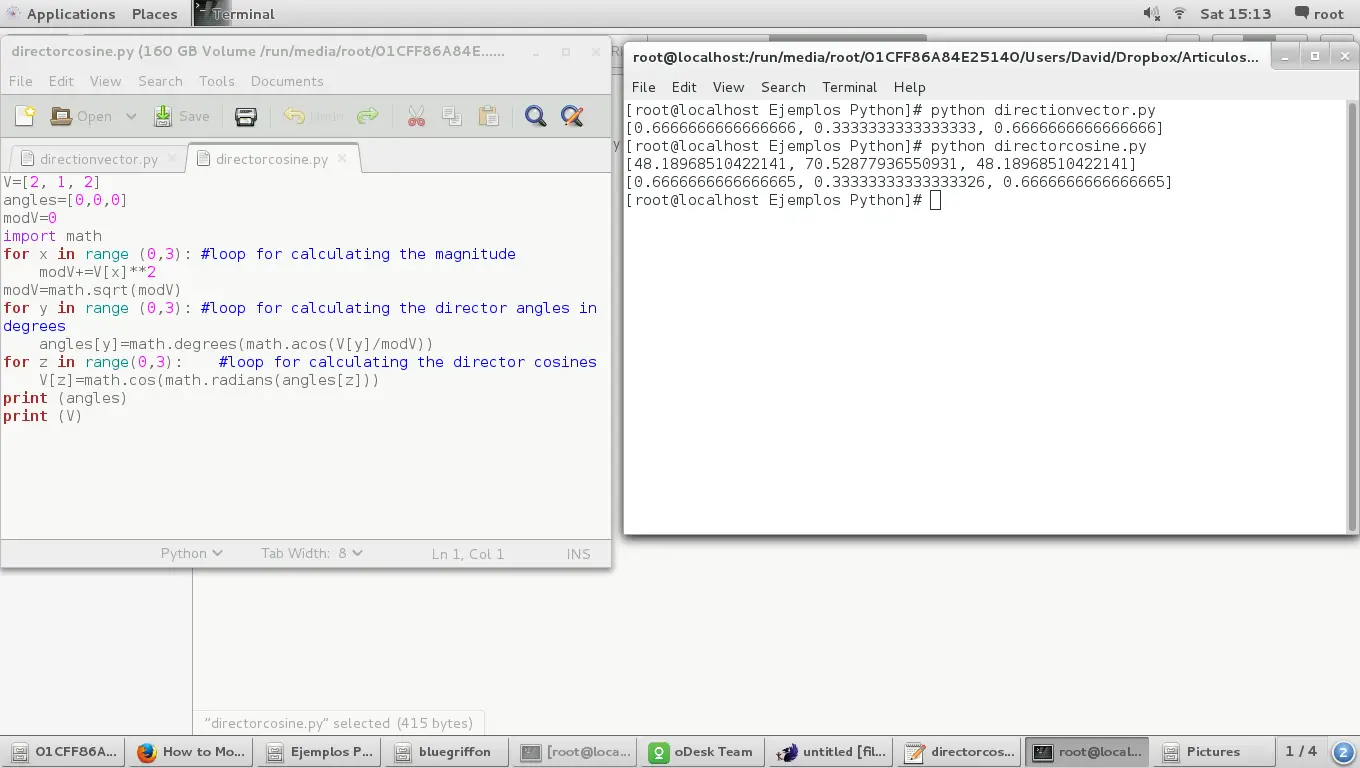
矢量的方向
如果我们改变一个向量所有坐标的符号,我们本质上就是在改变向量的方向,如下所示:
V=[-2, -1, -2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)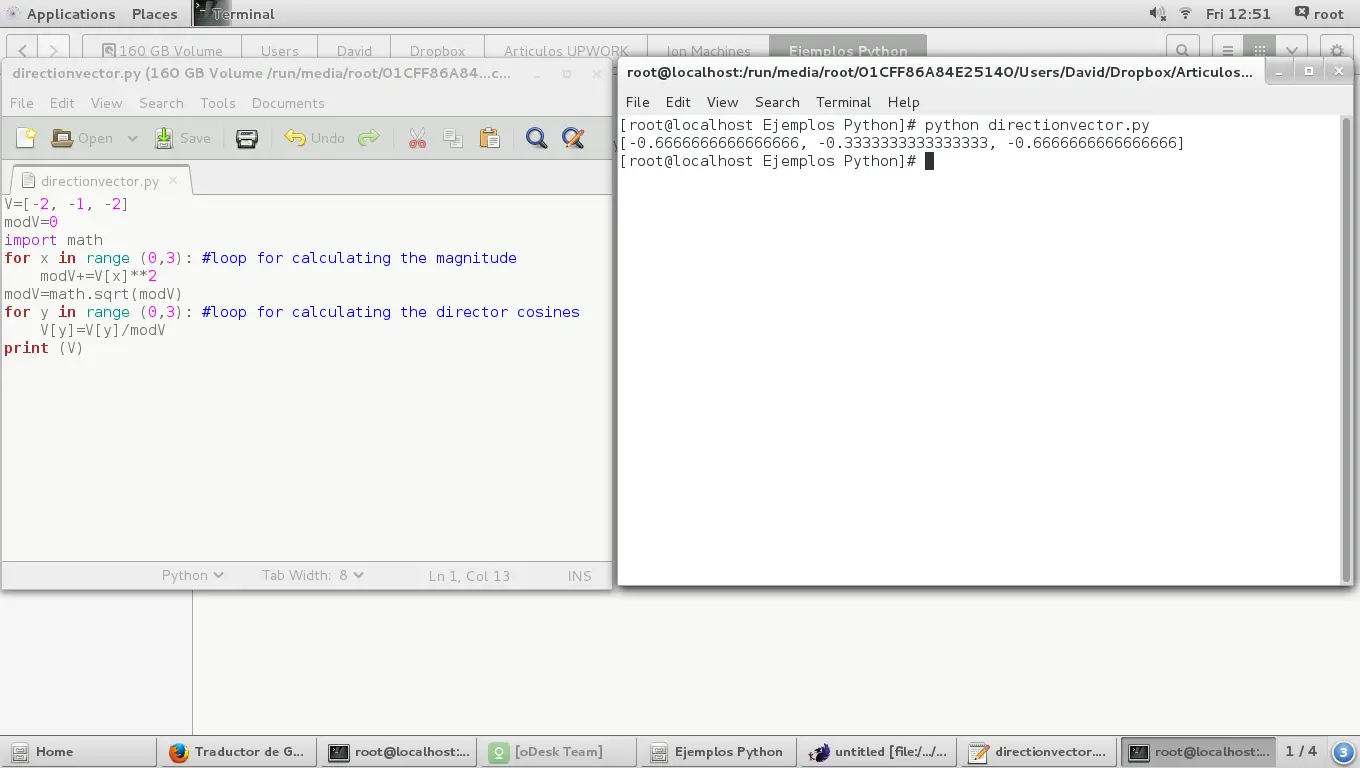
向量代数和
首先我们要声明代数和涉及的所有向量,如下:
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]我们要在哪里对 A 加 B 求和,结果将存储在 S 中
在 Python 中添加两个向量(列表)相当于为结果向量的每个坐标运行一个 for 循环,因此我们必须执行以下操作:
for x in range(0,3):
S[x]=A[x]+B[x]这里我们有代数向量和的完整脚本:
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
for x in range(0,3): #For loop for adding the homologue coordinate of each vector
S[x]=A[x]+B[x]
print 'S=',A, '+', B, '=', S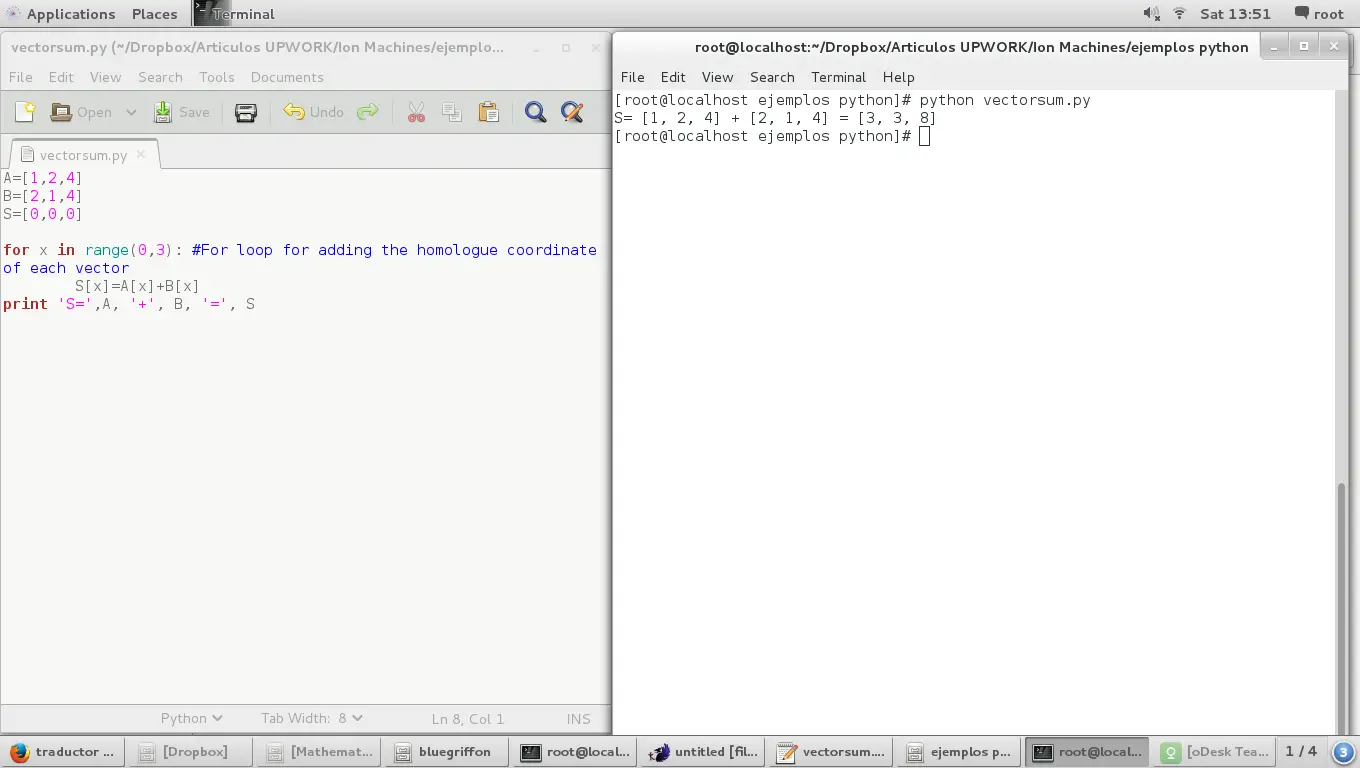
向量乘以标量
给定一个向量:
A=[1,-2,3]和一个标量:
scalar=-2标量的乘积向量定义为向量每个坐标的标量积:
for x in range(0,3):
R[x]=scalar*A[x]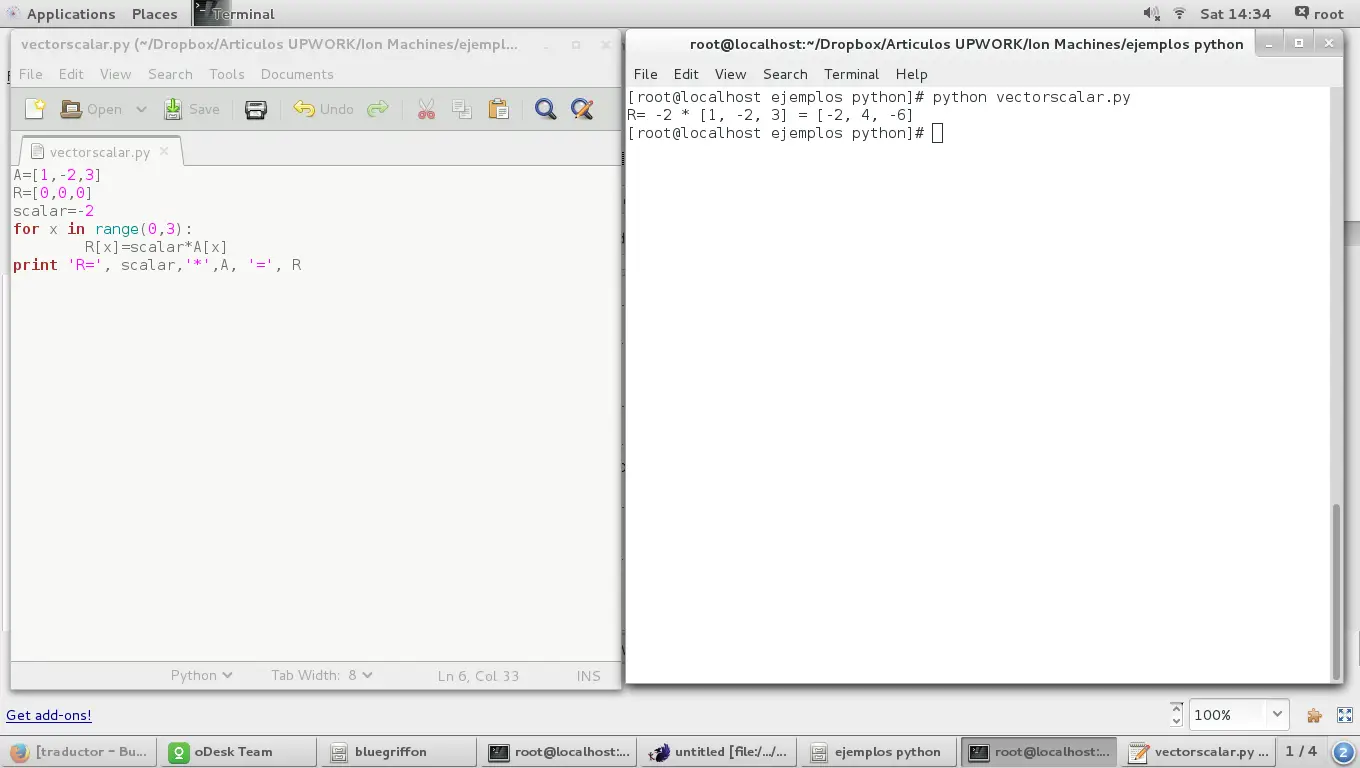
单位向量
使用向量脚本的幅度,我们有:
V=[2, 2, 1]
U=[0,0,0]
modV=0
invmodV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
invmodV=1/modV
for x in range(0,3):
U[x]=invmodV*V[x]
print 'U=',V,'/',modV,'=',U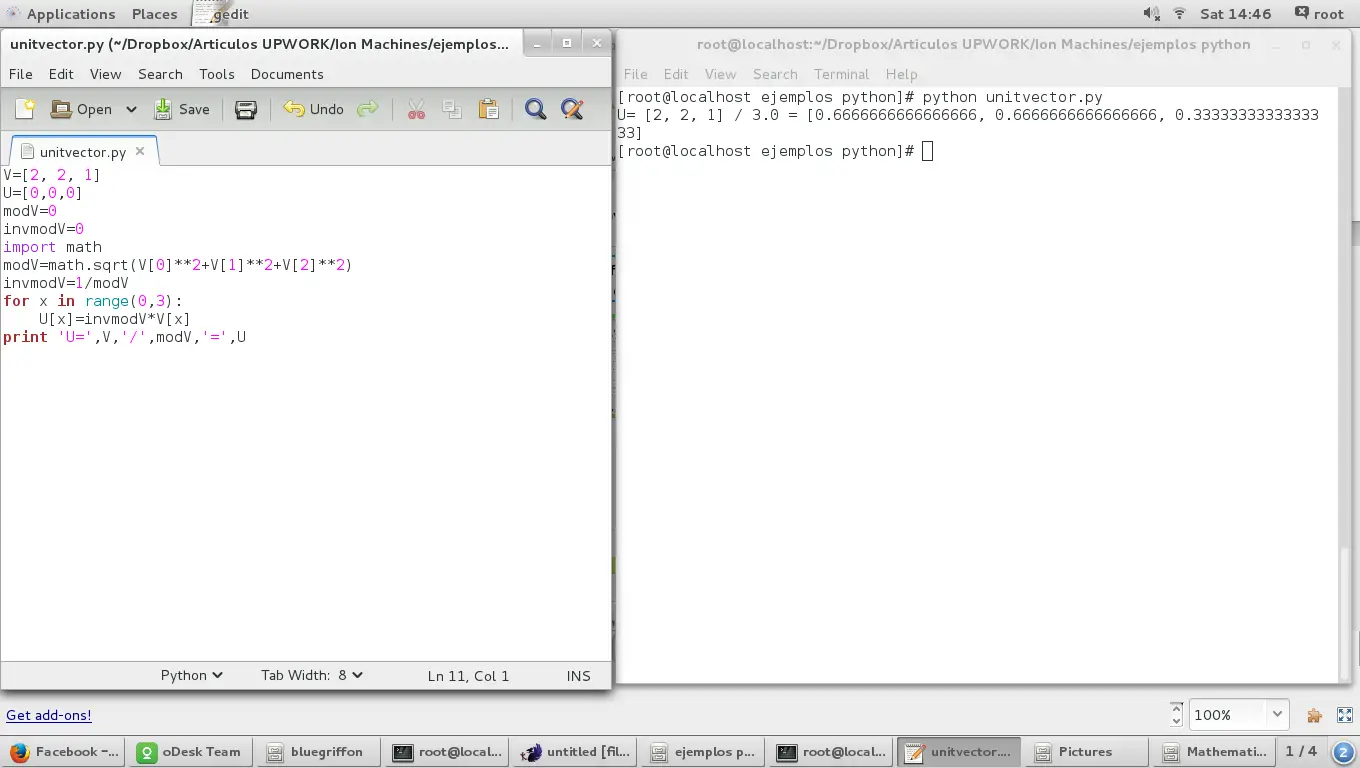
线性组合
给定三个向量 A、B 和 C,我们可以计算标量值,分别乘以 B 和 C 得到向量 A。换句话说,将向量 A 作为向量 B 和 C 的线性组合:
A=[7, 9, -8]
B=[1, 3, -2]
C=[-2, 0, 1]线性组合导致方程组,如果三个向量 r3 则有 3 个方程和 2 个变量(标量),或者如果它们是 R3 中的两个向量则有 2 个方程和 2 个变量,这可以通过应用矩阵的行列式来求解。由于 Python 处理的数据类型,这里我们必须指出一点。很多时候在计算线性组合中涉及的标量时,结果会有小数位,从而导致浮点运算。 Python 处理的数字数据类型是:Integer、Real、Long。所以,我们必须插入向量的坐标作为 Real 数据类型,所以这些代表实数(浮点数)。我们必须了解和理解Python中数据类型的一些特性:
- Integer 比 Real 类型占用更少的内存空间。
- 实数运算比整数运算慢。
这里我们有相同的向量,但声明为 Real 类型:
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]所以,有了这个我们可以交换向量,从而总是有系统解决方案。
我们要做的第一个检查是向量之间是否共面,从而知道是否存在线性组合。为此,我们将实施行列式矩阵:det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors如果此行列式等于零 (0),则向量之间存在线性相关性,我们可以继续计算标量。如上所述,方程组有两个变量的三个方程,产生一个确定的兼容系统,为此我们必须取三个方程中的两个并求解标量值,然后检查第三个方程,之前没有,如果前一个标量值解决它。如果他们不解决这个问题,那么就没有线性组合。
这里我们有完整的代码:A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
if det0==0:
det1=B[0]*C[1]-B[1]*C[0] #First Determinant involving the first and second lines of the equations system
if det1==0:
det2=B[1]*C[2]-B[2]*C[1] #Second Determinant involving the second and third lines of the equations system
if det2==0:
print 'Linear Combination Unexistent'
else:
det3=A[1]*C[2]-A[2]*C[1]
det4=B[1]*A[2]-B[2]*A[1]
sc1=det3/det2
sc2=det4/det2
if sc1*B[0]+sc2*C[0]==A[0]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
det3=A[0]*C[1]-A[1]*C[0]
det4=B[0]*A[1]-B[1]*A[0]
sc1=det3/det1
sc2=det4/det1
if sc1*B[2]+sc2*C[2]==A[2]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
print 'Linear Combination Unexistent'
结果:[ ejemplos python]#
总之,基本向量代数会导致一系列涉及线性方程组和/或简单实数算术的运算。在另一个教程中,我们将了解如何使用向量开发乘积,例如点积、叉积或混合积。
