科学音频处理，第二部分 - 如何使用带有 Octave 4.0 的 Ubuntu 对音频文件进行基本的数学信号处理

在此页

添加信号
1. 第 1 步：创建两个不同频率的信号（ogg 文件）
2. 第 2 步：添加两个信号
3. 第 3 步：添加两个真实信号（以两个音乐曲目为例）
1. 生成的产品信号图
2. 将基频差较大的两个信号相乘的图形效果（调制原理）
在之前的教程中，我们看到了读取、写入和播放音频文件的简单步骤。我们甚至看到了如何从余弦函数等周期函数合成音频文件。在本教程中，我们将了解如何对信号进行加法、乘法（调制）以及应用一些基本数学函数来查看它们对原始信号的影响。
添加信号
两个信号 S1(t) 和 S2(t) 的总和产生信号 R(t)，其在任何时刻的值都是该时刻相加信号值的总和。像这样：
R(t)=S1(t) + S2(t)
我们将在 Octave 中重新创建两个信号的总和，并以图形方式查看效果。首先，我们将生成两个不同频率的信号，以查看总和产生的信号。
第 1 步：创建两个不同频率的信号（ogg 文件）
```
>> sig1='cos440.ogg';                  %creating the audio file @440 Hz
>> sig2='cos880.ogg';                  %creating the audio file @880 Hz
>> fs=44100;                           %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1,cos(w1),fs);        %writing the function cos(w) on the files created
>> audiowrite(sig2,cos(w2),fs);
```
这里我们将绘制两个信号。
信号图 1 (440 Hz)
```
>> [y1, fs] = audioread(sig1);
>> plot(y1)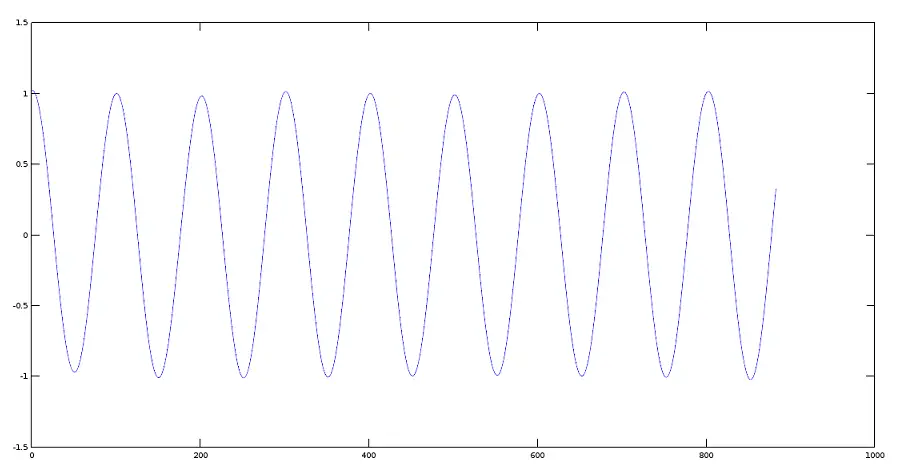
```
信号图 2 (880 Hz)
```
>> [y2, fs] = audioread(sig2);
>> plot(y2)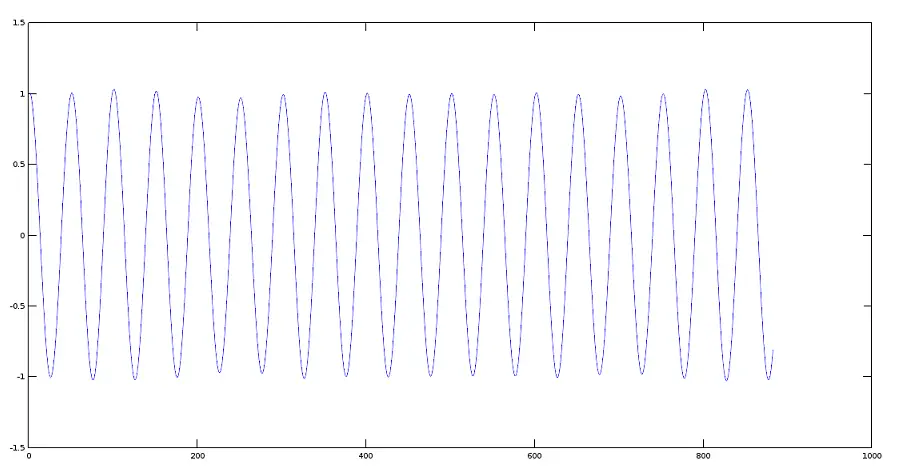
```
第 2 步：添加两个信号
现在我们执行上一步中创建的两个信号的总和。
```
>> sumres=y1+y2;
>> plot(sumres)
```
结果信号图
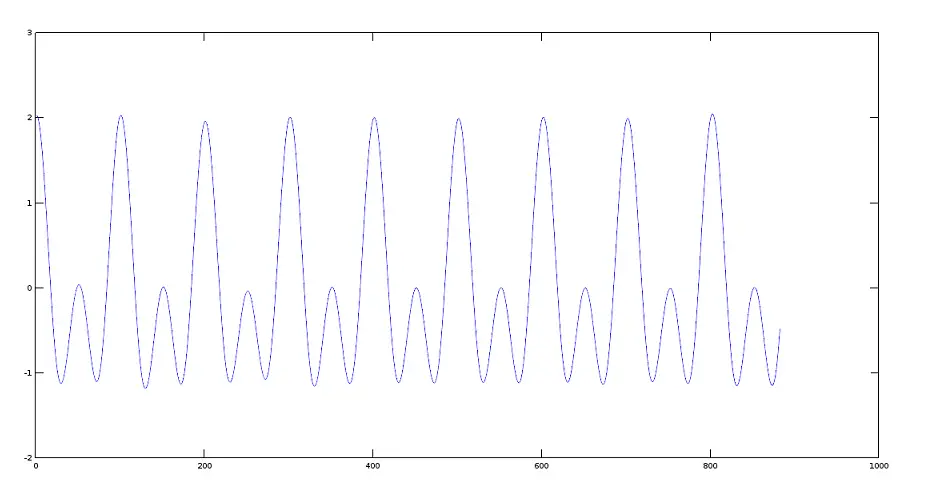
八度效应
在 Octaver 中，这种效果提供的声音是有特点的，因为它模拟了音乐家正在演奏的音符，无论是在较低的还是较高的八度音程中（根据它的编程），加上原始音符的声音，即出现两个音符听起来一样。
第 3 步：添加两个真实信号（以两个音乐曲目为例）
为此，我们将使用两首格里高利圣歌（语音采样）。
艾维玛利亚赛道
首先，将阅读并绘制 Avemaria 曲目：
```
>> [y1,fs]=audioread('avemaria_.ogg');
>> plot(y1)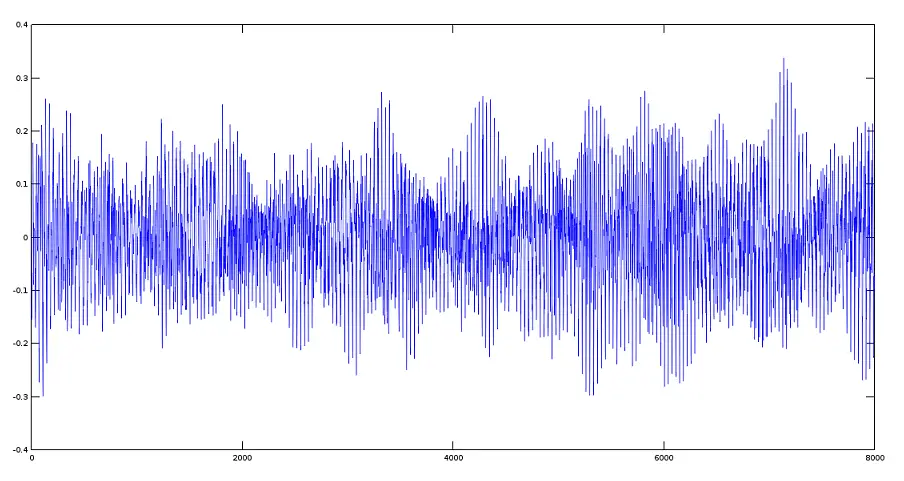
```
赞美诗曲目
现在，将阅读并绘制一首赞美诗曲目
```
>> [y2,fs]=audioread('hymnus.ogg');
>> plot(y2)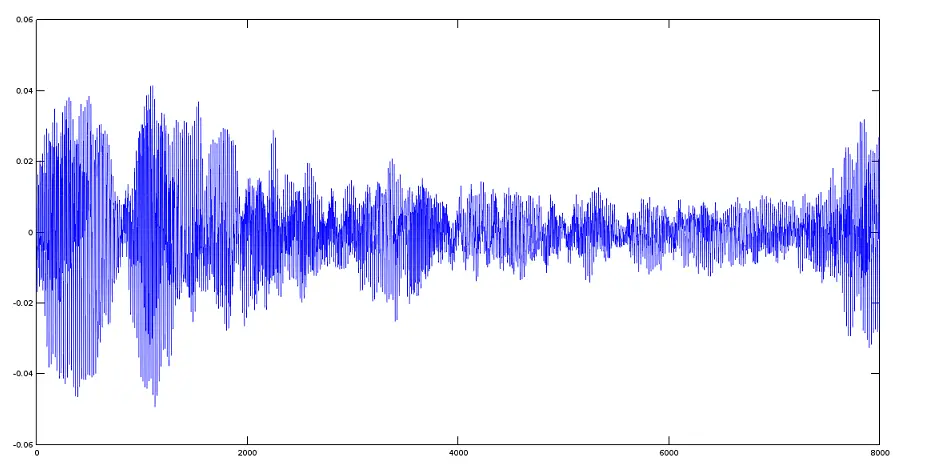
```
Avemaria + Hymnus 曲目
```
>> y='avehymnus.ogg';
>> audiowrite(y, y1+y2, fs);
>> [y, fs]=audioread('avehymnus.ogg');
>> plot(y)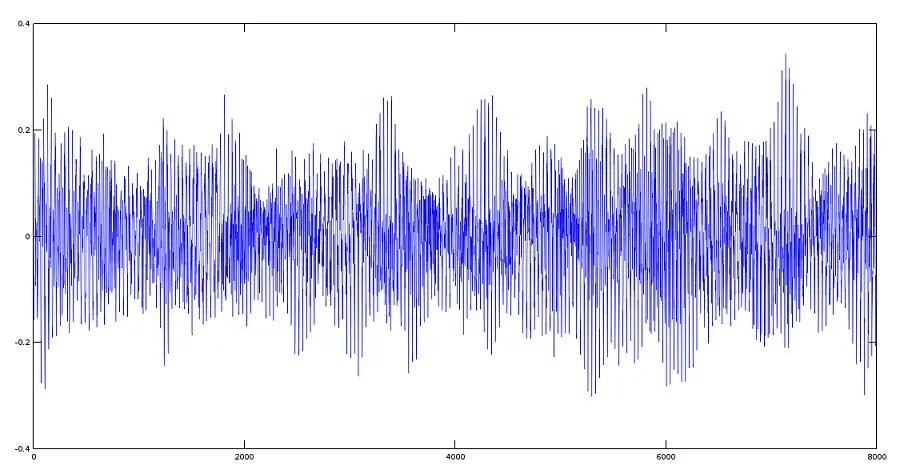
```
两个信号的乘积

要将两个信号相乘，我们必须使用类似求和的方法。让我们使用之前创建的相同文件。
```
>> sig1='cos440.ogg';                  %creating the audio file @440 Hz
>> sig2='cos880.ogg';                  %creating the audio file @880 Hz
>> product='prod.ogg';                 %creating the audio file for product
>> fs=44100;                           %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1, cos(w1), fs);      %writing the function cos(w) on the files created
>> audiowrite(sig2, cos(w2), fs);
>> [y1,fs]=audioread(sig1);
>> [y2,fs]=audioread(sig2);
>> audiowrite(product, y1.*y2, fs);    %performing the product
>> [yprod,fs]=audioread(product);
>> plot(yprod);                        %plotting the product
```
注意：我们必须使用操作数 .* 因为此产品是在参数文件上按值对值制作的。更多内容请参考Octave矩阵产品操作手册。
产生的产品信号图
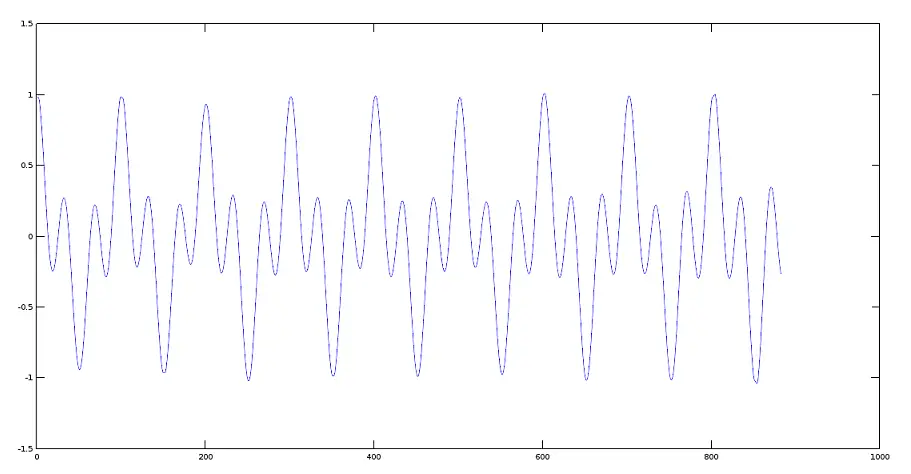
基频相差较大的两个信号相乘的图形效果（调制原理）
第1步：
创建频率为 220Hz 的音频信号。
```
>> fs=44100;
>> t=0:1/fs:0.03;
>> w=2*pi*220*t;
>> y1=cos(w);
>> plot(y1);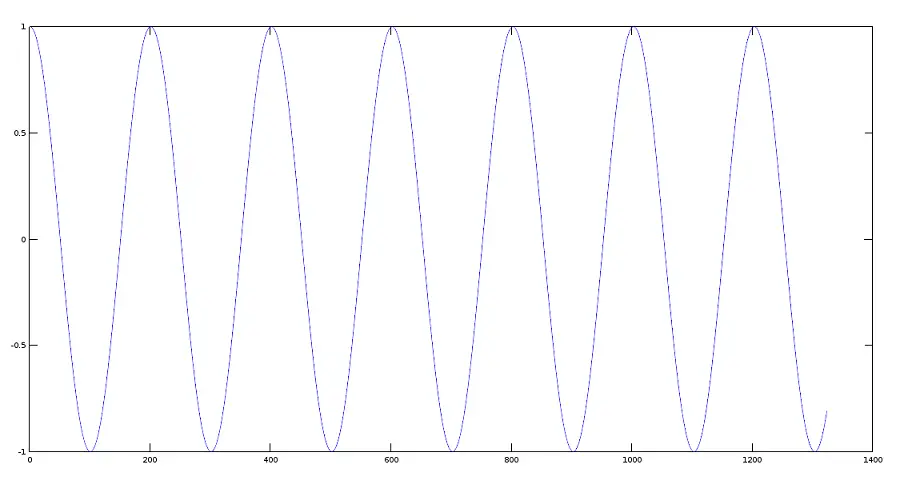
```
第2步：
创建 22000 Hz 的更高频率调制信号。
```
>> y2=cos(100*w);
>> plot(y2);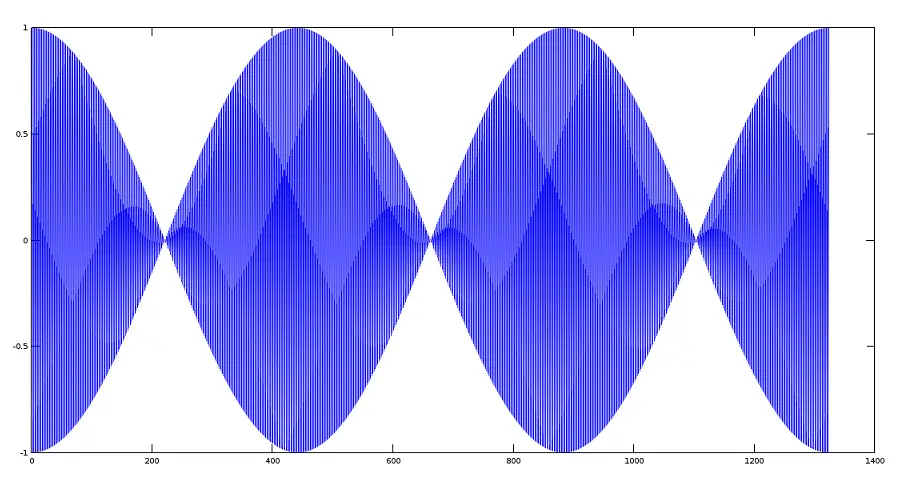
```
第 3 步：
将两个信号相乘并绘制。
```
>> plot(y1.*y2);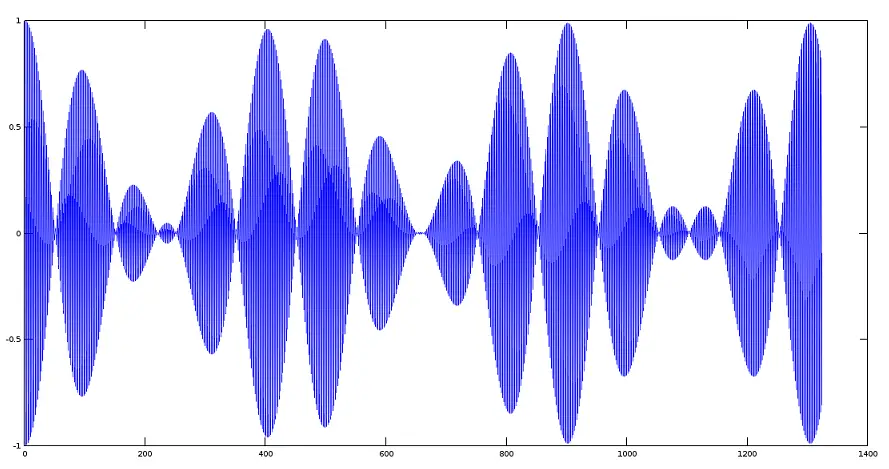
```
将信号乘以标量
将函数乘以标量的效果相当于修改它们的范围，在某些情况下，还修改相位的符号。给定标量 K，函数 F(t) 与标量的乘积定义为：
```
>> [y,fs]=audioread('cos440.ogg');        %creating the work files
>> res1='coslow.ogg';                
>> res2='coshigh.ogg';
>> res3='cosinverted.ogg';
>> K1=0.2;                                %values of the scalars
>> K2=0.5;
>> K3=-1;
>> audiowrite(res1, K1*y, fs);            %product function-scalar
>> audiowrite(res2, K2*y, fs);
>> audiowrite(res3, K3*y, fs);
```
```
>> plot(y)
```
振幅降低 0.2 的信号图
```
>> plot(res1)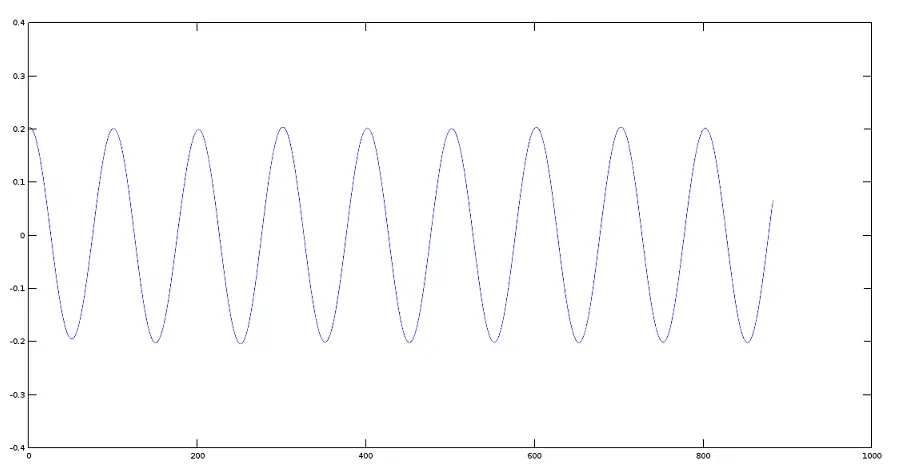
```
振幅降低 0.5 的信号图
```
>> plot(res2)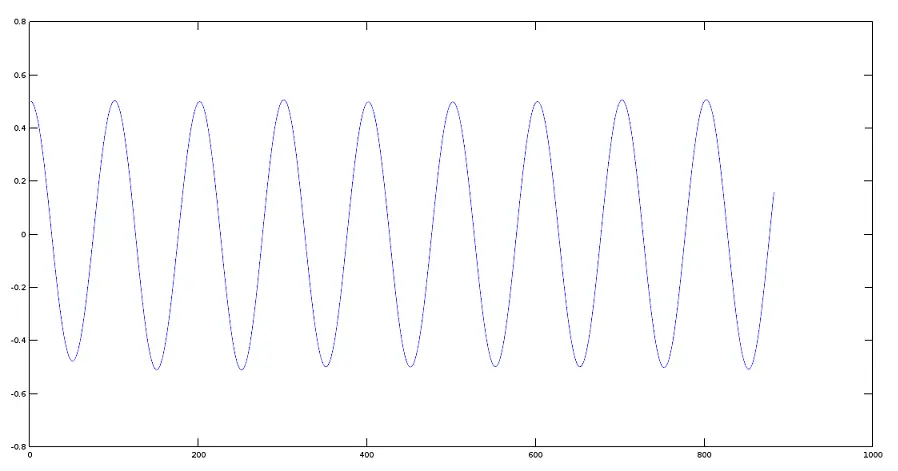
```
反相信号图
```
>> plot(res3)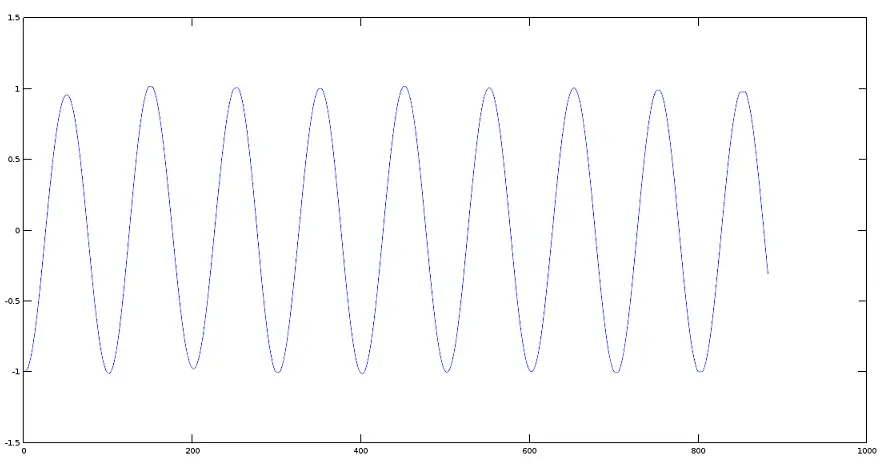
```
结论

基本的数学运算，例如函数的代数和、乘积和标量的乘积，是更高级运算的基础，其中包括频谱分析、幅度调制、角调制等。在下一个教程中，我们将看到如何进行此类操作及其对音频信号的影响。